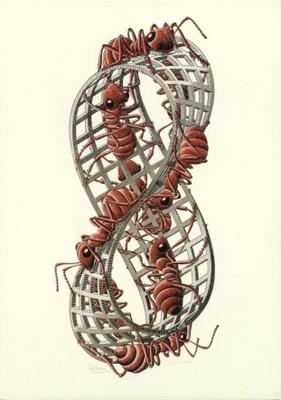
 Esta es la cinta que dibujó Escher, una cinta sin fin en la que las hormigas circulan indefinidamente por 'una y otra cara', es decir, por la misma cara. Cinta de Möbius II, 1963, xilografía en tres tintas.
Esta es la cinta que dibujó Escher, una cinta sin fin en la que las hormigas circulan indefinidamente por 'una y otra cara', es decir, por la misma cara. Cinta de Möbius II, 1963, xilografía en tres tintas.El sentido de la belleza de las matemáticas se remonta, por lo menos, a Pitágoras. La elegancia de una demostración, o la belleza de una fórmula puede ser suficiente para explicar su existencia. En este sentido, se manifestaba Apolonio de Perga (siglos II ó III antes de nuestra era), fue el creador de la formalización de las expresiones de las cónicas (elipse, hipérbola, parábola) como secciones del cono doble. En ese momento histórico, como en el nuestro, había adversarios de la Matemática pura que preguntaban con mala intención por la utilidad de tales resultados.
Hoy nadie le haría ningún reproche por su desarrollo de las Cónicas, sencillamente fundamentales en la Astronomía, la base de los diseños más vanguardistas en Arquitectura, fundamentales en el desarrollo de las telecomunicaciones, ¡quien no observó alguna vez las antenas parabólicas y agradeció la utilidad del “foco” como receptor de las ondas!.
Apolonio tuvo que defenderse en su época de los ataques de los “hombres prácticos”y afirmaba : “mis resultados en Geometría merecen ser aceptados a causa de sus propias demostraciones, de la misma manera que aceptamos muchas otras cosas en la Matemática por esta razón y por ninguna otra”
En este sentido os propongo que observéis la extraña geometría de la cinta de Möbius,sin cuestionar su utilidad.
August Ferdinand Möbius (1790-1868) nació en Schulpforta, Alemania. Fue discípulo de Gauss y ejerció como astrónomo y matemático en la Universidad de Leipzig. Fue uno de los pioneros de la Topología, área en que investigó las superficies de una sola cara, como su famosa cinta, descubierta en 1858. 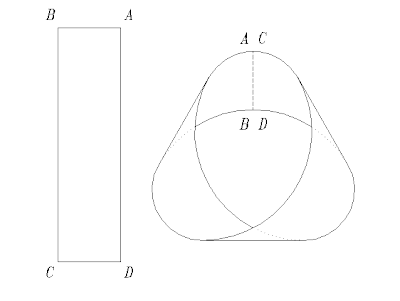 La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.
La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.  Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.
Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.  Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.
Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.
 La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.
La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.  Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.
Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.  Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.
Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.  Es increíble el poder de sugerencia que tiene la cinta de Moebius para los artistas. Esta escultura es un ejemplo de cinta de Möbius, en este caso tridimensional, se lo debemos a Max Bill (Winterthur, 1908-Berlín, 1994) pintor, escultor, arquitecto y diseñador gráfico suizo. Uno de los exponentes de los principios vanguardistas de la Bauhaus en Alemania tras el final de la I Guerra Mundial en 1918. Su insistencia en la utilización de una base matemática para toda forma de arte queda reflejada en sus pinturas, que se caracterizan por sus diseños con frecuencia geométricos. Entre 1935 y 1953 creó, en el campo de la escultura, diferentes variaciones sobre el tema del lazo infinito en metal pulido. Por si alguien se pasa por allí, una versión en piedra de esta obra ( Unendliche Schleife) se puede ver en el Centre Pompidou de París.
Es increíble el poder de sugerencia que tiene la cinta de Moebius para los artistas. Esta escultura es un ejemplo de cinta de Möbius, en este caso tridimensional, se lo debemos a Max Bill (Winterthur, 1908-Berlín, 1994) pintor, escultor, arquitecto y diseñador gráfico suizo. Uno de los exponentes de los principios vanguardistas de la Bauhaus en Alemania tras el final de la I Guerra Mundial en 1918. Su insistencia en la utilización de una base matemática para toda forma de arte queda reflejada en sus pinturas, que se caracterizan por sus diseños con frecuencia geométricos. Entre 1935 y 1953 creó, en el campo de la escultura, diferentes variaciones sobre el tema del lazo infinito en metal pulido. Por si alguien se pasa por allí, una versión en piedra de esta obra ( Unendliche Schleife) se puede ver en el Centre Pompidou de París. 

















1 comentario:
bien entre en tu espacio por interes en un imaginario ciclotron botella Klein --> Moebius 4-5 dimensional con acelaraciones u relativistas
tienes muy buenas selecciones
gracias
Publicar un comentario